A continuación se presenta un artículo detallado sobre las funciones recursivas en programación, con ejemplos, esquemas e imágenes explicativas. El artículo profundiza en los conceptos fundamentales, la aplicación práctica y los beneficios y limitaciones de la recursividad en distintos lenguajes de programación.
Funciones Recursivas en Programación: Un Análisis Profundo
La recursividad es una técnica fundamental en la programación que permite a una función llamarse a sí misma para resolver problemas complejos dividiéndolos en subproblemas más pequeños y manejables. Este método no solo es elegante desde el punto de vista conceptual, sino que, en ciertos casos, resulta ser la solución más intuitiva para problemas que implican estructuras repetitivas o datos anidados, como árboles y listas enlazadas. En este artículo, exploraremos en profundidad qué es la recursividad, cómo se implementa en distintos lenguajes, cuáles son sus ventajas y desventajas, y veremos ejemplos prácticos, además de incluir esquemas e imágenes que facilitan su comprensión.
Introducción a la Recursividad
La recursividad es un método de resolución de problemas en el que la solución de un problema depende de soluciones a instancias más pequeñas del mismo problema. En otras palabras, en lugar de resolver un problema de forma iterativa, se divide en subproblemas que se resuelven de manera similar. Este enfoque es especialmente útil para problemas naturalmente definidos de forma recursiva, como el cálculo de números factoriales, la exploración de estructuras jerárquicas y la generación de fractales.
Por ejemplo, el cálculo del factorial de un número nn se puede definir como:
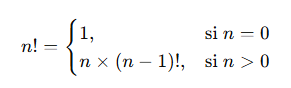
Este ejemplo muestra claramente la naturaleza autoinvocada del problema, en la que la solución para nn depende de la solución para n−1n-1.
Conceptos Básicos
Definición y Principios
La recursividad se fundamenta en dos componentes esenciales:
- Caso Base: Es la condición que permite detener la recursión. Sin un caso base, la función se llamaría indefinidamente y causaría un desbordamiento de pila (stack overflow).
- Caso Recursivo: Es la parte en la que la función se llama a sí misma con un conjunto de parámetros modificados, acercándose progresivamente al caso base.
Estos dos componentes aseguran que la función recursiva eventualmente se detenga, devolviendo una solución para el problema original.
Estructura de una Función Recursiva
Generalmente, la estructura de una función recursiva en pseudo-código es la siguiente:
funcion recursiva(parametro):
si (condición de término):
devolver valor_base
sino:
realizar alguna operación
llamar a recursiva(parametro_modificado)
En lenguajes de programación como Python, Java o C++, la implementación de esta estructura varía ligeramente en sintaxis, pero los principios son los mismos.
Ejemplos Prácticos
Factorial de un Número
El ejemplo clásico para ilustrar la recursividad es el cálculo del factorial de un número. En Python, una implementación recursiva podría verse así:
def factorial(n):
if n == 0:
return 1 # Caso base
else:
return n * factorial(n - 1) # Caso recursivo
# Ejemplo de uso:
print(factorial(5)) # Salida: 120
En este ejemplo, la función factorial se llama a sí misma con el argumento n-1 hasta que n alcanza 0, momento en el cual se detiene la recursión.
Serie de Fibonacci
Otro ejemplo clásico es la serie de Fibonacci, en la cual cada número es la suma de los dos anteriores. Una función recursiva para calcular el nn-ésimo término de la serie de Fibonacci puede definirse como:
def fibonacci(n):
if n <= 1:
return n # Caso base para n=0 o n=1
else:
return fibonacci(n - 1) + fibonacci(n - 2) # Llamadas recursivas
# Ejemplo de uso:
print(fibonacci(7)) # Salida: 13
Aunque esta implementación es intuitiva, su eficiencia puede ser cuestionable para valores grandes de nn debido a la cantidad de llamadas recursivas redundantes.
Recorrido de Árboles
La recursividad es especialmente útil para recorrer estructuras de datos jerárquicas, como árboles. Un ejemplo es el recorrido en preorden de un árbol binario:
class Nodo:
def __init__(self, valor):
self.valor = valor
self.izquierda = None
self.derecha = None
def recorrido_preorden(nodo):
if nodo:
print(nodo.valor) # Visitar el nodo actual
recorrido_preorden(nodo.izquierda) # Recorrer el subárbol izquierdo
recorrido_preorden(nodo.derecha) # Recorrer el subárbol derecho
# Ejemplo de creación de un árbol simple:
raiz = Nodo(1)
raiz.izquierda = Nodo(2)
raiz.derecha = Nodo(3)
raiz.izquierda.izquierda = Nodo(4)
raiz.izquierda.derecha = Nodo(5)
recorrido_preorden(raiz)
En este ejemplo, el recorrido preorden visita el nodo actual y luego recurre en sus subárboles, demostrando cómo la recursividad se adapta de forma natural a estructuras en árbol.
Ventajas y Desventajas de la Recursividad
Ventajas
- Simplicidad y Elegancia:
La recursividad permite resolver problemas complejos de manera sencilla y elegante. Por ejemplo, recorrer una estructura en árbol o generar combinaciones se vuelve intuitivo usando recursividad. - Reducción de Código:
Las soluciones recursivas suelen ser más cortas y fáciles de entender, ya que se enfocan en el problema en sí mismo, sin necesidad de escribir bucles anidados complejos. - Adaptabilidad a Problemas Jerárquicos:
Para estructuras de datos que son naturalmente jerárquicas, como los árboles y grafos, la recursividad es la herramienta ideal para realizar búsquedas, recorridos y transformaciones.
Desventajas
- Uso Intensivo de Memoria:
Cada llamada recursiva añade un marco en el stack de llamadas. En problemas con gran profundidad recursiva, esto puede llevar a un desbordamiento de pila (stack overflow). - Ineficiencia en Algunos Casos:
Algunas implementaciones recursivas, como la función de Fibonacci mostrada anteriormente, realizan muchas llamadas redundantes, lo que puede resultar en tiempos de ejecución exponenciales. - Complejidad en la Depuración:
Identificar errores en funciones recursivas puede ser más difícil, ya que el seguimiento de las llamadas anidadas requiere una comprensión profunda del flujo de ejecución. - Alternativas Iterativas:
Muchos problemas que se pueden resolver de manera recursiva también pueden ser resueltos mediante métodos iterativos que, en algunos casos, son más eficientes en términos de uso de memoria y velocidad.
Aplicaciones en la Programación Moderna
La recursividad se utiliza en una amplia variedad de aplicaciones modernas, abarcando desde algoritmos clásicos hasta técnicas avanzadas de procesamiento de datos y aprendizaje automático. Algunas aplicaciones destacadas incluyen:
1. Algoritmos de Búsqueda y Ordenación
- Búsqueda en Árboles y Grafos:
La recursividad se emplea para recorrer estructuras jerárquicas como árboles binarios, árboles de decisión y grafos. Algoritmos como el recorrido en preorden, inorden y postorden son implementaciones recursivas comunes. - Algoritmos de Ordenación:
Métodos como el quicksort y el mergesort se basan en la recursividad para dividir el conjunto de datos en partes más pequeñas y ordenarlas de forma independiente.
2. Procesamiento de Lenguaje Natural (NLP)
- Análisis Sintáctico:
En el análisis de lenguajes naturales y la construcción de árboles de sintaxis, la recursividad es esencial para interpretar y descomponer oraciones en sus componentes gramaticales. - Transformaciones de Texto:
Algunas transformaciones y búsquedas de patrones en textos se implementan de manera recursiva, especialmente cuando se trabaja con expresiones regulares o estructuras anidadas.
3. Gráficos y Computación Gráfica
- Generación de Fractales:
Los fractales, que son patrones geométricos infinitamente complejos, se generan de manera recursiva. Ejemplos famosos incluyen el conjunto de Mandelbrot y el triángulo de Sierpinski. - Renderizado de Escenas:
En ciertos algoritmos de renderizado, la recursividad ayuda a calcular la iluminación y el sombreado mediante el trazado de rayos, donde cada rayo de luz puede generar subrayos de forma recursiva.
4. Inteligencia Artificial y Juegos
- Búsqueda en Espacios de Estado:
Algoritmos como el minimax, usados en juegos de estrategia, exploran recursivamente posibles movimientos en el árbol de decisiones del juego. - Optimización y Programación Dinámica:
Muchas soluciones a problemas de optimización utilizan la recursividad en conjunto con técnicas de memorización para evitar cálculos redundantes, mejorando la eficiencia global del algoritmo.
Optimización y Técnicas Avanzadas
Debido a las desventajas inherentes a la recursividad, se han desarrollado varias técnicas para optimizar estas implementaciones. Algunas de las más relevantes son:
Recursión de Cola (Tail Recursion)
La recursión de cola es una forma de recursividad en la que la llamada recursiva es la última operación que se realiza en la función. Esto permite a algunos compiladores y lenguajes de programación optimizar la llamada, reutilizando el marco de la función actual en lugar de crear uno nuevo. Por ejemplo, en lenguajes como Scheme o en implementaciones optimizadas en C, la recursión de cola evita el crecimiento del stack de llamadas.
Ejemplo en Python (aunque Python no optimiza automáticamente la recursión de cola):
def factorial_tail(n, acumulador=1):
if n == 0:
return acumulador
else:
return factorial_tail(n - 1, acumulador * n)
print(factorial_tail(5)) # Salida: 120
Programación Dinámica
La programación dinámica es una técnica que se combina a menudo con la recursividad para almacenar (o memorizar) resultados parciales y evitar cálculos redundantes. Este enfoque es fundamental en problemas de optimización y en algoritmos que resuelven subproblemas repetitivos, como el cálculo eficiente de la serie de Fibonacci.
Ejemplo de memorización en la función Fibonacci:
def fibonacci_mem(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fibonacci_mem(n - 1, memo) + fibonacci_mem(n - 2, memo)
return memo[n]
print(fibonacci_mem(50))
Recursividad vs. Iteración
Si bien la recursividad puede ofrecer soluciones elegantes, muchas veces se compara con la iteración en términos de eficiencia. En algunos lenguajes o situaciones, una solución iterativa puede ser preferible debido a la menor sobrecarga de llamadas. Sin embargo, es importante considerar que, en muchos casos, la claridad y mantenibilidad del código recursivo compensan su menor eficiencia, especialmente cuando se implementan optimizaciones como la recursión de cola o la memorización.
Consideraciones Prácticas en el Uso de la Recursividad
Para aprovechar al máximo las funciones recursivas, es importante tener en cuenta algunas recomendaciones:
- Definir Claramente el Caso Base:
Asegúrese de que cada función recursiva tenga un caso base que detenga la recursión. La ausencia de un caso base correcto puede resultar en bucles infinitos y desbordamiento de pila. - Evitar Cálculos Redundantes:
En problemas donde se pueden calcular varias veces los mismos subproblemas, utilice técnicas de memorización o recursión de cola para mejorar la eficiencia. - Realizar Pruebas Exhaustivas:
Dado que las funciones recursivas pueden ser difíciles de depurar, es esencial realizar pruebas unitarias y utilizar técnicas de depuración (por ejemplo, trazas de pila) para asegurarse de que cada llamada se comporta como se espera. - Comparar con Soluciones Iterativas:
En algunos escenarios, es beneficioso analizar si una solución iterativa puede ofrecer una mejora en el rendimiento sin sacrificar la claridad del código. La elección entre recursión e iteración depende del problema específico y de las limitaciones del entorno de ejecución.
Recursividad en Diferentes Lenguajes de Programación
La recursividad se implementa de formas similares en muchos lenguajes, aunque cada uno tiene sus peculiaridades:
Python
Python permite una implementación directa de la recursividad, pero su límite de recursión predeterminado puede requerir ajustes para problemas muy profundos. Se puede modificar este límite mediante el módulo sys:
import sys
sys.setrecursionlimit(3000)
Sin embargo, se recomienda usar recursión de forma moderada en Python para evitar problemas de rendimiento.
Java
En Java, la recursividad es una herramienta común, aunque, como en otros lenguajes, es importante gestionar el uso de la pila. Las llamadas recursivas pueden ser optimizadas por el compilador en algunos casos, pero no de forma tan agresiva como en lenguajes funcionales.
C/C++
En C y C++, la recursividad es ampliamente utilizada en algoritmos clásicos. La eficiencia de la recursión depende en gran medida del compilador y de la optimización del código. Se recomienda una gestión cuidadosa de la memoria, especialmente en sistemas embebidos o con recursos limitados.
Lenguajes Funcionales
Lenguajes como Haskell, Scheme y Erlang están diseñados para aprovechar al máximo la recursividad. La recursión de cola es una característica estándar y se optimiza de forma nativa, permitiendo escribir código elegante y altamente eficiente.
Casos de Uso Reales y Ejemplos Avanzados
La recursividad no es solo una herramienta teórica, sino que se utiliza en aplicaciones del mundo real. Algunos ejemplos avanzados incluyen:
Algoritmos de Búsqueda en Inteligencia Artificial
En el desarrollo de juegos y sistemas de inteligencia artificial, la recursividad se emplea para explorar posibles movimientos o estados. El algoritmo minimax, por ejemplo, utiliza recursividad para evaluar jugadas en juegos como el ajedrez o el tic-tac-toe, calculando la mejor jugada a partir de un árbol de decisiones.
Generación Procedural de Contenidos
En el desarrollo de videojuegos y simulaciones, la recursividad permite generar paisajes, mazmorras y estructuras de forma procedural. Por ejemplo, el algoritmo de subdivisión recursiva se utiliza para crear terrenos realistas a partir de patrones fractales.
Análisis de Datos y Procesamiento de Árboles de Decisión
En el campo de la ciencia de datos, la recursividad es fundamental para construir y recorrer árboles de decisión, utilizados en algoritmos de clasificación y regresión. Estos árboles, generados a partir de datos, se recorren recursivamente para tomar decisiones basadas en criterios de división.
Diagramas Conceptuales Adicionales
Para complementar la comprensión de la recursividad, a continuación se presentan dos diagramas adicionales:
Esquema Conceptual de una Función Recursiva
flowchart TD
A[Inicio] --> B[Evaluar condición de término]
B -- Caso base --> C[Devolver resultado]
B -- Caso recursivo --> D[Realizar operación]
D --> E[Llamada recursiva con parámetro modificado]
E --> F[Recibir resultado de la llamada]
F --> G[Procesar y devolver resultado final]
Descripción:
Este diagrama, realizado con Mermaid, muestra de forma conceptual el flujo de una función recursiva, desde la evaluación de la condición de término hasta la llamada recursiva y la devolución del resultado.
Visualización de la Evolución del Stack de Llamadas
sequenceDiagram
participant Main as Función Principal
participant R1 as Llamada Recursiva 1
participant R2 as Llamada Recursiva 2
participant Rn as Llamada Recursiva n
Main->>R1: Llamar a la función recursiva
R1->>R2: Llamada interna
R2->>Rn: Llamada interna hasta llegar al caso base
Note right of Rn: Caso base alcanzado<br/>comienza el retorno
Rn-->>R2: Retorno del resultado
R2-->>R1: Retorno del resultado
R1-->>Main: Retorno final
Descripción:
Este diagrama de secuencia ilustra cómo se acumulan y luego se liberan los marcos en el stack de llamadas a medida que la recursividad avanza y luego retrocede al alcanzar el caso base.
Conclusión
La recursividad es una herramienta poderosa y versátil en la programación, permitiendo la solución de problemas complejos mediante la descomposición en subproblemas más simples. Desde el cálculo del factorial y la serie de Fibonacci hasta la generación de estructuras complejas y la exploración de árboles de decisión, la recursividad se adapta a múltiples escenarios y lenguajes de programación.
Aunque presenta algunas limitaciones, como el uso intensivo de memoria y posibles ineficiencias en ciertos casos, sus ventajas en términos de claridad y adaptabilidad la hacen indispensable para muchos algoritmos. Además, técnicas avanzadas como la recursión de cola y la memorización permiten mitigar algunas de estas desventajas, haciendo que la recursividad sea una opción viable incluso en aplicaciones de alto rendimiento.
En el contexto de la programación moderna, la recursividad sigue siendo un pilar fundamental, ya sea en el desarrollo de software, la inteligencia artificial o el análisis de datos. Dominar este concepto no solo enriquece el repertorio del programador, sino que también abre la puerta a la comprensión de estructuras y algoritmos que, de otra forma, resultarían difíciles de implementar de forma iterativa.
Reflexiones Finales
La práctica de la recursividad requiere una mentalidad distinta a la de los bucles iterativos tradicionales. Es importante aprender a visualizar la ejecución de una función recursiva, comprender la importancia de un caso base bien definido y reconocer cuándo es más eficiente optar por una solución iterativa. Con el tiempo, el dominio de la recursividad se convierte en una herramienta invaluable en el arsenal del desarrollador, permitiéndole abordar problemas complejos con soluciones elegantes y efectivas.
Esperamos que este artículo haya contribuido a una comprensión profunda y detallada de las funciones recursivas en programación, proporcionándole tanto la teoría como ejemplos prácticos y esquemas visuales que faciliten el aprendizaje de este poderoso concepto.