A continuación se presenta un artículo detallado sobre la complejidad algorítmica, donde se abordan las notaciones Big O, Big Omega (Ω) y Big Theta (Θ). El texto incluye definiciones teóricas, ejemplos prácticos y fragmentos de código para ilustrar cómo se aplican estos conceptos en el análisis de algoritmos.

Comprendiendo la Complejidad Algorítmica: Big O, Big Omega y Big Theta

La complejidad algorítmica es una herramienta fundamental en el análisis de algoritmos, ya que permite medir y comparar la eficiencia de distintos métodos para resolver un problema. En un mundo donde los datos y la optimización son claves, comprender y analizar la eficiencia de un algoritmo se vuelve indispensable para diseñar soluciones escalables y robustas. En este artículo, profundizaremos en las tres notaciones más utilizadas para medir la complejidad: Big O (O), Big Omega (Ω) y Big Theta (Θ). Se explicarán sus definiciones formales, se contrastarán sus usos y se brindarán ejemplos y código para una comprensión práctica.

1. Introducción a la Complejidad Algorítmica

1.1 ¿Por qué es importante medir la complejidad?

Cuando diseñamos un algoritmo, uno de los aspectos más críticos es saber cómo se comportará conforme el tamaño de la entrada aumenta. Por ejemplo, un algoritmo de búsqueda lineal puede funcionar bien para listas pequeñas, pero a medida que la cantidad de datos crece, su rendimiento puede degradarse significativamente. Conocer la complejidad algorítmica nos permite predecir el tiempo de ejecución y el consumo de recursos, lo que es crucial en aplicaciones donde el rendimiento es vital.

1.2 Conceptos básicos

El análisis de algoritmos se centra en estudiar dos aspectos principales:

Complejidad temporal: Representa el tiempo que tarda un algoritmo en ejecutarse en función del tamaño de la entrada.
Complejidad espacial: Representa la cantidad de memoria adicional que utiliza el algoritmo.

Generalmente, cuando hablamos de complejidad, nos referimos a la complejidad temporal, aunque en ocasiones es necesario considerar también el uso de memoria.

2. Notación Big O (O Grande)

2.1 Definición formal

La notación Big O se utiliza para describir un límite superior asintótico del comportamiento de un algoritmo. Formalmente, decimos que una función f(n) es O(g(n)) si existen constantes positivas c y n0 tales que para todo n ≥ n0 se cumple:

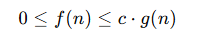
Esto significa que, para valores grandes de n, f(n) no crecerá más rápido que una constante multiplicada por g(n).

2.2 Ejemplos comunes de Big O

O(1): Tiempo constante. Un algoritmo que siempre tarda lo mismo, sin importar el tamaño de la entrada.
O(n): Tiempo lineal. El tiempo de ejecución crece proporcionalmente al tamaño de la entrada.
O(n²): Tiempo cuadrático. Algoritmos que tienen dos bucles anidados, donde el tiempo de ejecución crece proporcionalmente al cuadrado del tamaño de la entrada.
O(log n): Tiempo logarítmico. Algoritmos que reducen el tamaño del problema en cada iteración, como la búsqueda binaria.

2.3 Ejemplo práctico en código: Búsqueda lineal

A continuación, se muestra un ejemplo en Python de un algoritmo de búsqueda lineal, cuyo tiempo de ejecución es O(n):

def busqueda_lineal(lista, objetivo):
    """
    Busca el objetivo en la lista de forma lineal.
    Retorna el índice si lo encuentra, o -1 si no está presente.
    """
    for indice, elemento in enumerate(lista):
        if elemento == objetivo:
            return indice
    return -1

# Ejemplo de uso:
numeros = [5, 3, 7, 1, 9, 2]
resultado = busqueda_lineal(numeros, 7)
print("Índice del elemento buscado:", resultado)

En este ejemplo, en el peor de los casos se recorren todos los elementos de la lista, por lo que la complejidad es O(n).

3. Notación Big Omega (Ω)

3.1 Definición formal

La notación Big Omega (Ω) se utiliza para describir un límite inferior asintótico del comportamiento de un algoritmo. Formalmente, decimos que f(n) es Ω(g(n)) si existen constantes positivas c y n0 tales que para todo n ≥ n0:

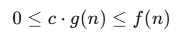
Esto significa que f(n)f(n) crecerá al menos tan rápido como c⋅g(n)c \cdot g(n) para nn suficientemente grande.

3.2 Interpretación práctica

La notación Big Omega nos dice que, sin importar cuán optimizado esté un algoritmo, siempre tomará al menos una cierta cantidad de tiempo en función del tamaño de la entrada. Es útil para establecer el rendimiento mínimo que podemos esperar.

3.3 Ejemplo práctico: Búsqueda en el mejor caso

En el algoritmo de búsqueda lineal, aunque el peor de los casos es O(n), el mejor de los casos se considera Ω(1), pues si el elemento buscado está en la primera posición, el algoritmo se detendrá inmediatamente. Considera el siguiente ejemplo:

def busqueda_lineal_mejor_caso(lista, objetivo):
    """
    Realiza una búsqueda lineal, considerando el mejor caso.
    Retorna el índice si lo encuentra, o -1 en caso contrario.
    """
    if lista and lista[0] == objetivo:
        return 0
    # En el peor de los casos, realiza la búsqueda completa.
    for indice, elemento in enumerate(lista):
        if elemento == objetivo:
            return indice
    return -1

# Ejemplo de uso:
numeros = [10, 20, 30, 40, 50]
resultado = busqueda_lineal_mejor_caso(numeros, 10)
print("Índice del elemento buscado:", resultado)

En este caso, si el elemento se encuentra en la primera posición, el algoritmo tendrá una complejidad de Ω(1).

4. Notación Big Theta (Θ)

4.1 Definición formal

La notación Big Theta (Θ) se utiliza para describir una cota ajustada del comportamiento asintótico de un algoritmo. Se dice que f(n) es Θ(g(n)) si existen constantes positivas c1, c2 y n0 tales que para todo n≥n0:

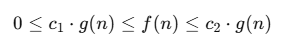
Esto implica que g(n)g(n) es una descripción asintótica exacta del comportamiento de f(n)f(n); es decir, f(n)f(n) crece a la misma tasa que g(n)g(n) para nn suficientemente grande.

4.2 Ejemplos y su relevancia

Considera un algoritmo cuya complejidad en el peor de los casos es O(n) y en el mejor caso es Ω(n). En este escenario, podemos afirmar que la complejidad del algoritmo es Θ(n), ya que ambos límites, superior e inferior, son lineales.

Un ejemplo típico es el algoritmo de búsqueda secuencial en una lista no ordenada, donde en el peor de los casos se recorre toda la lista y, en promedio, se recorre la mitad de ella. Sin embargo, si consideramos una implementación en la que siempre se analiza la misma cantidad de operaciones (por ejemplo, en ciertos algoritmos de procesamiento de datos donde cada elemento se procesa exactamente una vez), se tiene una complejidad Θ(n).

4.3 Ejemplo práctico en código

Veamos un ejemplo en Python donde procesamos cada elemento de una lista una sola vez:

def procesar_lista(lista):
    """
    Procesa cada elemento de la lista realizando una operación constante.
    Se asume que cada operación toma el mismo tiempo.
    """
    suma = 0
    for elemento in lista:
        # Operación constante por cada elemento
        suma += elemento
    return suma

# Ejemplo de uso:
numeros = list(range(1, 101))  # Lista con 100 elementos
resultado = procesar_lista(numeros)
print("Resultado de la suma:", resultado)

En este ejemplo, cada elemento se procesa exactamente una vez, lo que implica que la complejidad temporal es Θ(n).

5. Comparación entre O, Ω y Θ

5.1 Cuándo usar cada notación

Big O (O grande): Se utiliza para describir la cota superior de un algoritmo. Es ideal para garantizar que un algoritmo no se comportará peor que cierta tasa de crecimiento.
Big Omega (Ω): Se usa para describir la cota inferior. Es útil para identificar el tiempo mínimo que se espera en el mejor de los casos.
Big Theta (Θ): Proporciona una cota ajustada, es decir, describe el comportamiento exacto (tanto superior como inferior) del algoritmo para entradas grandes.

5.2 Ejemplo comparativo

Consideremos el algoritmo de ordenamiento por burbuja (Bubble Sort). En el peor de los casos, el algoritmo tiene una complejidad O(n²), ya que se realizan comparaciones y posibles intercambios para cada par de elementos en una lista de tamaño n. Sin embargo, en el mejor de los casos—cuando la lista ya está ordenada—Bubble Sort puede detectar la ausencia de intercambios y detenerse, logrando una complejidad Ω(n). Aun así, dado que los dos límites no coinciden, no podemos afirmar que su complejidad sea Θ(n); el comportamiento típico se encuentra en algún punto intermedio, y en análisis asintótico se sigue describiendo como O(n²) en el peor caso.

6. Aplicación de la Complejidad en Problemas Reales

6.1 Análisis de algoritmos en la práctica

En la práctica, el análisis de la complejidad algorítmica ayuda a:

Elegir el algoritmo adecuado: Para problemas con grandes volúmenes de datos, algoritmos con complejidad polinomial de alto grado o exponencial pueden ser inviables.
Optimizar código: Identificar cuellos de botella y secciones del código que requieren optimización.
Diseño de sistemas escalables: Asegurarse de que el sistema se comportará adecuadamente a medida que la carga o la cantidad de datos aumente.

6.2 Ejemplo: Búsqueda binaria

La búsqueda binaria es un ejemplo clásico de un algoritmo eficiente, ya que reduce a la mitad el tamaño del problema en cada iteración, logrando una complejidad O(log n). A continuación, se muestra una implementación en Python:

def busqueda_binaria(lista, objetivo):
    """
    Realiza una búsqueda binaria en una lista ordenada.
    Retorna el índice del objetivo si se encuentra, o -1 si no está presente.
    """
    inicio = 0
    fin = len(lista) - 1

    while inicio <= fin:
        medio = (inicio + fin) // 2
        if lista[medio] == objetivo:
            return medio
        elif lista[medio] < objetivo:
            inicio = medio + 1
        else:
            fin = medio - 1
    return -1

# Ejemplo de uso:
numeros_ordenados = list(range(1, 101))
resultado = busqueda_binaria(numeros_ordenados, 73)
print("Índice del elemento buscado:", resultado)

La búsqueda binaria es un ejemplo perfecto de cómo reducir el número de operaciones mediante la división del espacio de búsqueda, lo que se traduce en un comportamiento logarítmico.

6.3 Ejemplo: Algoritmo de ordenamiento Merge Sort

El algoritmo Merge Sort es un ejemplo de algoritmo eficiente que utiliza la técnica divide y vencerás. Su complejidad es O(n log n) en el peor de los casos. Se puede implementar de la siguiente manera en Python:

def merge_sort(lista):
    """
    Ordena una lista utilizando el algoritmo Merge Sort.
    """
    if len(lista) > 1:
        mitad = len(lista) // 2
        izquierda = lista[:mitad]
        derecha = lista[mitad:]

        # Ordena recursivamente ambas mitades
        merge_sort(izquierda)
        merge_sort(derecha)

        # Mezcla las dos mitades ordenadas
        i = j = k = 0
        while i < len(izquierda) and j < len(derecha):
            if izquierda[i] < derecha[j]:
                lista[k] = izquierda[i]
                i += 1
            else:
                lista[k] = derecha[j]
                j += 1
            k += 1

        # Agrega los elementos restantes de izquierda, si existen
        while i < len(izquierda):
            lista[k] = izquierda[i]
            i += 1
            k += 1

        # Agrega los elementos restantes de derecha, si existen
        while j < len(derecha):
            lista[k] = derecha[j]
            j += 1
            k += 1

# Ejemplo de uso:
numeros = [38, 27, 43, 3, 9, 82, 10]
merge_sort(numeros)
print("Lista ordenada:", numeros)

Merge Sort es altamente valorado por su eficiencia y estabilidad en el ordenamiento, especialmente cuando se trabaja con grandes volúmenes de datos.

7. Herramientas y Técnicas para el Análisis de Complejidad

7.1 Notación asintótica y límites

El análisis asintótico se centra en el comportamiento de las funciones conforme nn tiende a infinito. Esto permite ignorar constantes y términos de menor orden, lo que resulta en una simplificación que refleja la tendencia de crecimiento real del algoritmo. Las herramientas matemáticas involucradas incluyen:

Límites: Permiten establecer la relación entre dos funciones para n→∞.
Teorema del Sandwich: Utilizado en la definición de Θ, para acotar una función entre dos cotas.
Límites superior e inferior: Esenciales para definir Big O y Big Omega, respectivamente.

7.2 Análisis empírico vs. teórico

El análisis teórico se basa en la matemática para determinar la complejidad asintótica. Sin embargo, en la práctica, también es útil realizar un análisis empírico mediante pruebas y benchmarks. Este enfoque combinado ayuda a:

Validar supuestos teóricos: Mediante experimentación y pruebas en casos reales.
Identificar factores ocultos: Como la sobrecarga de llamadas a funciones o la administración de memoria, que no siempre se reflejan en la notación asintótica.

7.3 Herramientas de profiling

Existen diversas herramientas que ayudan a medir el rendimiento de un algoritmo en la práctica. Algunas de las más populares en Python son:

cProfile: Permite perfilar el tiempo de ejecución de cada función.
timeit: Útil para medir el tiempo de ejecución de pequeños fragmentos de código.
line_profiler: Permite perfilar línea por línea el rendimiento de una función.

Un ejemplo de uso de timeit:

import timeit

codigo = '''
def suma_lineal(lista):
    total = 0
    for numero in lista:
        total += numero
    return total

lista = list(range(1000))
suma_lineal(lista)
'''

tiempo = timeit.timeit(codigo, number=1000)
print("Tiempo de ejecución:", tiempo)

Estas herramientas permiten detectar cuellos de botella y optimizar algoritmos de manera práctica.

8. Consideraciones Avanzadas en el Análisis de Complejidad

8.1 Mejor, peor y caso promedio

Un aspecto importante del análisis de algoritmos es distinguir entre:

Mejor caso (best-case): La situación en la que el algoritmo ejecuta el mínimo número de operaciones.
Peor caso (worst-case): La situación en la que se requiere el máximo número de operaciones.
Caso promedio (average-case): Una estimación del comportamiento del algoritmo en situaciones “normales” o con entradas aleatorias.

Por ejemplo, en la búsqueda lineal, el mejor caso es Ω(1) si el elemento buscado se encuentra en la primera posición, mientras que el peor caso es O(n) si el elemento está ausente o en la última posición.

8.2 Análisis amortizado

El análisis amortizado es una técnica que se utiliza para obtener una medida promedio del costo de una operación a lo largo de una secuencia de operaciones. Aunque una operación individual pueda tener un costo alto, el costo amortizado puede resultar bajo cuando se distribuye a lo largo de muchas operaciones. Un ejemplo clásico es la implementación dinámica de arreglos (por ejemplo, listas en Python), donde la operación de redimensionamiento es costosa, pero se distribuye entre muchas inserciones.

8.3 Complejidad en algoritmos recursivos

Los algoritmos recursivos, como Merge Sort o Quick Sort, a menudo se analizan utilizando la recurrencia y el teorema maestro. Este teorema proporciona una forma sistemática de resolver recurrencias de la forma:

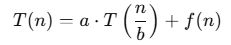
donde aa y bb son constantes y f(n) representa el costo del trabajo realizado en cada llamada. Este método permite establecer cotas asintóticas precisas para muchos algoritmos recursivos.

9. Ejemplos Prácticos y Estudios de Caso

9.1 Ordenamiento por inserción (Insertion Sort)

El algoritmo de ordenamiento por inserción es otro ejemplo instructivo para el análisis de la complejidad. Su comportamiento es:

Peor caso: O(n²), cuando la lista está en orden inverso.
Mejor caso: Ω(n), cuando la lista ya está ordenada.
Caso promedio: Θ(n²).

A continuación se muestra un ejemplo en Python:

def insertion_sort(lista):
    """
    Ordena la lista utilizando el algoritmo de ordenamiento por inserción.
    """
    for i in range(1, len(lista)):
        clave = lista[i]
        j = i - 1
        # Mueve los elementos de lista[0..i-1] que son mayores que clave
        # una posición hacia adelante
        while j >= 0 and lista[j] > clave:
            lista[j + 1] = lista[j]
            j -= 1
        lista[j + 1] = clave
    return lista

# Ejemplo de uso:
numeros = [12, 11, 13, 5, 6]
print("Lista ordenada:", insertion_sort(numeros))

Este algoritmo es sencillo de implementar y resulta eficiente para listas pequeñas o parcialmente ordenadas.

9.2 Análisis de algoritmos en estructuras de datos

La complejidad algorítmica también es crucial en el diseño y análisis de estructuras de datos. Por ejemplo:

Listas enlazadas: Las operaciones de inserción y eliminación pueden realizarse en O(1) si se tiene una referencia directa al nodo, pero la búsqueda en una lista enlazada es O(n).
Árboles binarios de búsqueda: La búsqueda, inserción y eliminación tienen una complejidad promedio de O(log n) si el árbol está balanceado, pero pueden degradarse a O(n) en el peor caso.
Tablas hash: En promedio, las operaciones de inserción, búsqueda y eliminación tienen complejidad O(1), aunque pueden degradarse a O(n) en casos de colisiones excesivas.

Estos ejemplos resaltan la importancia de elegir la estructura de datos adecuada para garantizar un rendimiento óptimo en función de las operaciones que se van a realizar.

10. Conclusión

El análisis de la complejidad algorítmica es una disciplina esencial en el campo de la informática y la ingeniería de software. A lo largo de este artículo, hemos explorado las notaciones Big O, Big Omega y Big Theta, que permiten caracterizar el comportamiento de los algoritmos en el límite para entradas de gran tamaño. Hemos visto que:

Big O proporciona una cota superior, asegurando que el algoritmo no se comportará peor que cierto límite.
Big Omega establece una cota inferior, indicando el rendimiento mínimo en el mejor de los casos.
Big Theta ofrece una descripción ajustada del comportamiento asintótico, cuando ambas cotas coinciden.

Además, a través de ejemplos prácticos y fragmentos de código, se ha demostrado cómo aplicar estos conceptos en algoritmos comunes como la búsqueda lineal, la búsqueda binaria, el ordenamiento por inserción, Bubble Sort y Merge Sort. El análisis teórico se complementa con herramientas prácticas que permiten validar la eficiencia del algoritmo en escenarios reales, haciendo uso de técnicas de profiling y análisis empírico.

Comprender estos conceptos no solo es fundamental para desarrollar algoritmos eficientes, sino también para optimizar aplicaciones y sistemas que manejan grandes volúmenes de datos. La selección de la estructura de datos adecuada, la aplicación de técnicas de análisis amortizado y la evaluación cuidadosa de los casos de mejor, peor y promedio son aspectos que permiten diseñar soluciones escalables y robustas.

En resumen, el dominio de la complejidad algorítmica permite al desarrollador tomar decisiones informadas, elegir algoritmos que se adapten a las necesidades del problema y optimizar recursos computacionales. El estudio y aplicación de estas notaciones es una habilidad clave para cualquier profesional en el campo de la computación, ya que impacta directamente en la calidad y eficiencia de los sistemas desarrollados.

Esperamos que este artículo haya proporcionado una visión clara y completa de la complejidad algorítmica y las notaciones Big O, Big Omega y Big Theta, así como de su aplicación práctica en el análisis de algoritmos. La comprensión de estos conceptos es un paso fundamental en el camino hacia la optimización y el diseño de soluciones eficientes en el mundo de la informática.

Referencias y Lecturas Adicionales

Para profundizar en estos temas, se recomienda explorar los siguientes recursos:

«Introduction to Algorithms» de Cormen, Leiserson, Rivest y Stein: Un clásico que abarca una amplia variedad de algoritmos y técnicas de análisis.
«Algorithm Design Manual» de Steven S. Skiena: Un libro práctico que ofrece consejos y estrategias para la implementación y análisis de algoritmos.

La capacidad para analizar y comprender la complejidad de los algoritmos es esencial para el desarrollo de software de alta calidad y para la solución de problemas en entornos reales. Con el conocimiento de Big O, Big Omega y Big Theta, los ingenieros y desarrolladores pueden diseñar algoritmos que no solo funcionen correctamente, sino que también sean eficientes y escalables a medida que el tamaño de los datos y la demanda del sistema aumenten.

Resumen Final

El análisis de la complejidad algorítmica mediante las notaciones Big O, Big Omega y Big Theta es una herramienta indispensable en la evaluación y optimización de algoritmos. Con estas notaciones se pueden establecer límites asintóticos que describen el comportamiento de un algoritmo en función del tamaño de la entrada, permitiendo predecir y mejorar el rendimiento del software.

A lo largo de este artículo, se han presentado definiciones formales, ejemplos prácticos y fragmentos de código en Python para ilustrar cómo se puede aplicar este análisis en situaciones reales. Desde la búsqueda lineal y la búsqueda binaria hasta algoritmos de ordenamiento como Merge Sort e Insertion Sort, cada ejemplo ha mostrado la importancia de considerar tanto el mejor caso como el peor caso en el análisis de eficiencia.

El dominio de estos conceptos no solo permite optimizar el rendimiento del código, sino también tomar decisiones informadas sobre el diseño de algoritmos y estructuras de datos en proyectos a gran escala. Así, comprender la complejidad algorítmica se erige como una habilidad crítica para cualquier desarrollador o científico de la computación que aspire a crear soluciones eficientes y sostenibles en el tiempo.

Con este conocimiento, es posible abordar desafíos cada vez mayores en el procesamiento de datos y en la resolución de problemas complejos, asegurando que las aplicaciones y sistemas sean capaces de manejar la creciente demanda y el volumen de información en la era digital.

Complejidad algorítmica (O, Ω, Θ)